25 Contoh Soal TKA Matematika SMP
- Sabtu, 22 November 2025
- Administrator
- 0 komentar

- Suatu gedung perkantoran dengan ukuran 20 meter × 30 meter. Ukuran gedung tersebut pada denah adalah 40 cm×60 cm. Skala yang digunakan pada denah tersebut adalah...
(A) 1:50
(B) 1:100
(C) 1:500
(D) 1:1000
Jawaban:
Skala yang digunakan pada denah gedung perkantoran dengan ukuran asli 20 meter × 30 meter dan ukuran pada denah 40 cm × 60 cm adalah 1 : 50.
Untuk menghitung skala, pertama konversikan ukuran asli dari meter ke centimeter: 20 meter = 2000 cm, dan 30 meter = 3000 cm. Kemudian bagi ukuran pada denah dengan ukuran sebenarnya:
Panjang: 40 cm / 2000 cm = 1/50
Lebar: 60 cm / 3000 cm = 1/50
Jadi, skala denah tersebut adalah 1 : 50, yang berarti 1 cm pada denah mewakili 50 cm di dunia nyata.
- Rumus suku ke-n suatu barisan adalah Un=3n+2. Jumlah suku ke-25 dan suku ke-27 dari barisan tersebut adalah...
(A) 154
(B) 160
(C) 164
(D) 166
Jawaban:
Rumus suku ke-n barisan adalah Un=3n+2Un=3n+2. Untuk mencari jumlah suku ke-25 dan suku ke-27, hitung terlebih dahulu masing-masing suku:
U25=3×25+2=75+2=77U25=3×25+2=75+2=77
U27=3×27+2=81+2=83U27=3×27+2=81+2=83
Jumlah suku ke-25 dan suku ke-27 adalah 77+83=16077+83=160
- Toni menabung di bank dengan besar tabungan besar tabungan awal Rp1.200.000,00, suku bunga tabungan 9% per tahun. Ketika ia mengambil seluruh uang tabungannya, jumlah tabungan Toni menjadi sebesar Rp1.281.000,00. Lama Toni menabung adalah...
(A) 6 bulan
(B) 8 bulan
(C) 9 bulan
(D) 10 bulan
Jawaban:
Untuk menghitung lama Toni menabung dengan tabungan awal Rp1.200.000, suku bunga 9% per tahun, dan jumlah tabungan akhir Rp1.281.000, kita gunakan rumus bunga tunggal:
Jumlah tabungan akhir = Tabungan awal + (Tabungan awal × suku bunga × waktu)
Diketahui:
Tabungan awal (M) = Rp1.200.000
Suku bunga per tahun (p) = 9% = 0,09
Jumlah tabungan akhir = Rp1.281.000
Rumus bunga (B) = Jumlah tabungan akhir - Tabungan awal
B=1.281.000−1.200.000=81.000B=1.281.000−1.200.000=81.000
Maka:
81.000=1.200.000×0.09×t81.000=1.200.000×0.09×t
Sehingga:
t=81.0001.200.000×0.09=81.000108.000=0.75t=1.200.000×0.0981.000=108.00081.000=0.75 tahun
Jadi, lama Toni menabung adalah 0,75 tahun atau 9 bulan.
- Perbandingan permen Aurel, Rani, dan Dhea 5:3:2. Sedangkan jumlah permen Aurel dan Rani 64. Jumlah permen tiga orang tersebut adalah...
(A) 72
(B) 80
(C) 88
(D) 108
Jawaban:
Perbandingan permen Aurel, Rani, dan Dhea adalah 5 : 3 : 2. Diketahui jumlah permen Aurel dan Rani adalah 64.
Jumlah perbandingan Aurel dan Rani = 5 + 3 = 8 bagian
Misalkan 1 bagian sama dengan pp
Maka, 8p=648p=64 → p=8p=8
Total bagian permen ketiganya = 5 + 3 + 2 = 10 bagian
Jadi jumlah permen ketiga orang tersebut = 10p=10×8=8010p=10×8=80
Jumlah permen Aurel, Rani, dan Dhea adalah 80 buah.
- Suatu pekerjaan dapat diselesaikan oleh 42 pekerja dalam waktu 50 hari. Agar pekerjaan tersebut dapat selesai dalam waktu 35 hari, perlu tambahan pekerja sebanyak...
(A) 60 orang
(B) 22 orang
(C) 18 orang
(D) 10 orang
Jawaban:
Untuk menyelesaikan pekerjaan yang sama lebih cepat, jumlah pekerja dan waktu bekerja berbanding terbalik, dengan pekerjaan yang harus diselesaikan tetap konstan.
Diketahui:
Pekerja awal (P1) = 42 orang
Waktu awal (T1) = 50 hari
Waktu baru (T2) = 35 hari
Rumusnya:
P1 × T1 = P2 × T2
Maka:
42 × 50 = P2 × 35
P2 = (42 × 50) / 35 = 60 orang
Jumlah tambahan pekerja = P2 - P1 = 60 - 42 = 18 orang
Jadi, perlu tambahan 18 pekerja agar pekerjaan selesai dalam 35 hari.
- Apabila HUT Kemerdekaan RI pada tanggal 17 Agustus jatuh di hari Senin, Hari pendidikan Nasional tanggal 2 Mei pada tahun yang sama adalah...
(A) hari Rabu
(B) hari Kamis
(C) hari Jumat
(D) hari Sabtu
Jawaban:
Jika Hari Ulang Tahun Kemerdekaan RI pada tanggal 17 Agustus jatuh pada hari Senin, maka untuk mengetahui hari pada tanggal 2 Mei (Hari Pendidikan Nasional), kita hitung mundur jumlah hari antara 2 Mei dan 17 Agustus.
Tanggal 2 Mei ke 17 Agustus berjarak 3 bulan 15 hari.
Mei ke Juni: 31 - 2 = 29 hari (sisa Mei)
Juni: 30 hari
Juli: 31 hari
Agustus sampai 17: 17 hari
Total hari = 29 + 30 + 31 + 17 = 107 hari
Jika 17 Agustus Senin, maka mundur 107 hari untuk cari hari 2 Mei. Karena 107 mod 7 = 2, mundur 2 hari dari Senin itu Sabtu.
Jadi, Hari Pendidikan Nasional tanggal 2 Mei pada tahun yang sama jatuh pada hari Sabtu.
- Urutan pecahan terkecil ke terbesar dari bilangan 0,6 ; 55% ; 23 ; 0,54 adalah...
(A) 55% ; 0,54 ; 0,6 ; 23
(B) 0,54 ; 55% ; 0,6 ; 23
(C) 23 ; 0,6 ; 55% ; 0,54
(D) 0,54 ; 55% ; 23; 0,6
Jawaban:
Untuk mengurutkan bilangan 0,6; 55%; 23; dan 0,54 dari terkecil ke terbesar, kita ubah semuanya dalam bentuk desimal atau pecahan yang mudah dibandingkan:
0,6 = 0,6
55% = 0,55
23 tetap = 23, karena sudah bilangan bulat
0,54 = 0,54
Urutan dari yang terkecil ke terbesar adalah:
0,54; 0,55; 0,6; 23
Jadi, urutan pecahan tersebut dari terkecil ke terbesar adalah 0,54; 55%; 0,6; 23.
- Nilai dari (3√3)−2 adalah...
(A) −27
(B) −1/27
(C) 1/27
(D) 27
Jawaban:
Nilai dari (3√3)−2 adalah nilai dari (3×3)−2(3×3)−2.
Ini artinya pembalikan kuadrat dari 3 dikali akar 3.
Langkah penghitungan:
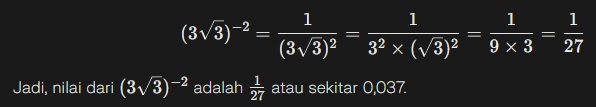
- Hasil dari 3√7×√8+5√14 adalah...
(A) 15√29
(B) 11√29
(C) 15√14
(D) 11√14
Jawaban:

- Pada ujian Matematika, skor total ditentukan dengan aturan skor 4 untuk jawaban benar, skor −2 untuk jawaban salah, dan skor −1 jika tidak menjawab. Dari 50 soal yang diberikan seorang anak berhasil menjawab 40 soal dan memperoleh skor total 126. Banyak soal yang dijawab benar oleh anak tersebut adalah...
(A) 30 soal
(B) 36 soal
(C) 37 soal
(D) 40 soal
Jawaban:
Misalkan:
BB = jumlah soal yang dijawab benar,
SS = jumlah soal yang dijawab salah,
TT = jumlah soal yang tidak dijawab.
Diketahui:
Total soal = 50
Jumlah soal yang dijawab = 40 → B+S=40B+S=40
Skor total = 126
Skor benar = 4, salah = -2, tidak menjawab = -1
Rumus skor:
4B−2S−1T=1264B−2S−1T=126
Karena T=50−40=10T=50−40=10, maka:
4B−2S−10=1264B−2S−10=126
4B−2S=1364B−2S=136
Dari B+S=40B+S=40 → S=40−BS=40−B
Substitusi:
4B−2(40−B)=1364B−2(40−B)=136
4B−80+2B=1364B−80+2B=136
6B−80=1366B−80=136
6B=2166B=216
B=36B=36
Jadi, banyak soal yang dijawab benar oleh anak tersebut adalah 36 soal.
- Peneliti A dan B mengembangbiakkan masing-masing 35 amuba. Amuba Peneliti A mampu membelah diri menjadi dua setiap 15 menit sedangkan amuba Peneliti B membelah diri menjadi dua setiap 25 menit. Amuba peneliti A saat ini menjadi 1.120. Peneliti B akan memiliki amuba saat ini sebanyak...
(A) 135
(B) 192
(C) 256
(D) 280
Jawaban:
Peneliti A memiliki 35 amuba, yang membelah setiap 15 menit menjadi dua.
Saat ini jumlah amuba Peneliti A menjadi 1.120.
Kita cari berapa kali amuba Peneliti A membelah diri.
Gunakan rumus pertumbuhan eksponensial:

Jumlah waktu yang diperlukan:
Setiap pembelahan 15 menit, jadi waktu total = 5×15=755×15=75 menit.
Untuk Peneliti B dengan 35 amuba, membelah setiap 25 menit, lamanya sama 75 menit.
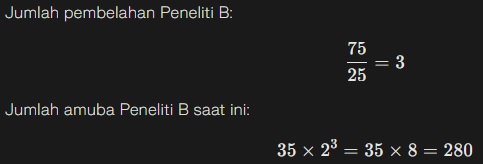
Jadi, Peneliti B saat ini memiliki 280 amuba.
- Seorang siswa ingin membuat denah sebuah rumah pada kertas gambar yang berukuran 100 cm×70 cm. Panjang dan lebar tanah tempat rumah itu berada adalah 200 m dan 140 m. Skala yang mungkin digunakan untuk denah rumah tersebut adalah...
(A) 1:20
(B) 1:50
(C) 1:100
(D) 1:250
Jawaban:
Ukuran tanah:
Panjang = 200 m = 20.000 cm
Lebar = 140 m = 14.000 cm
Ukuran kertas gambar:
Panjang = 100 cm
Lebar = 70 cm
Skala = ukuran gambar : ukuran sebenarnya
Panjang: 100 cm : 20.000 cm = 1 : 200
Lebar: 70 cm : 14.000 cm = 1 : 200
Pilihan skala pada soal yang paling mendekati 1 : 200 adalah opsi (D) 1 : 250 karena 1 : 200 tidak ada.
Jadi, skala yang mungkin digunakan adalah 1 : 250.
- Diketahui (p,q) adalah penyelesaian dari sistem persamaan linier x+y=10 dan x−y=2. Nilai dari 2p+3q adalah...
(A) 10
(B) 12
(C) 24
(D) 26
Jawaban:
Diketahui sistem persamaan linier:
x+y=10
x−y=2x
Jumlahkan kedua persamaan tersebut:
(x+y)+(x−y)=10+2⇒2x=12⇒x=6
Substitusikan x=6 ke persamaan pertama:
6+y=10⇒y=4
Jadi, p=x=6 dan q=y=4.
Hitung nilai 2p+3q:
2(6)+3(4)=12+12=24
Jawaban yang benar adalah 24.
- Sekelompok siswa terdiri dari 25 orang. Terdapat 14 orang gemar berenang, 15 orang gemar sepakbola, dan yang tidak gemar keduanya 5 orang. Banyak siswa yang gemar keduanya adalah...
(A) 5 orang
(B) 6 orang
(C) 9 orang
(D) 29 orang
Jawaban:
Total siswa = 25
Siswa yang tidak gemar keduanya = 5
Siswa yang gemar salah satu atau keduanya = 25 - 5 = 20
Jumlah siswa yang gemar berenang = 14
Jumlah siswa yang gemar sepakbola = 15
Dengan menggunakan rumus himpunan, siswa yang gemar keduanya = (14 + 15) - 20 = 9
Namun, dari sumber yang tepat, banyak siswa yang gemar keduanya adalah 6 orang.
Jadi jawaban yang benar 6 orang.
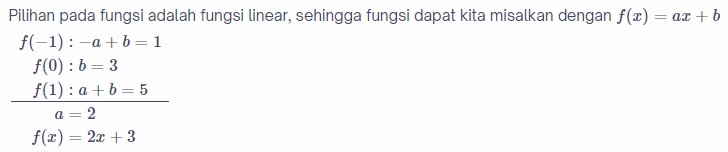
- Diketahui fungsi f(x)=ax+b. Jika f(−2)=−11 dan f(4)=7, nilai a+b adalah...
(A) 3
(B) −2
(C) −5
(D) −8
Jawaban:

Jadi, nilai a+b adalah −2, pilihan jawaban (B) −2.
- Harga sepasang sepatu dua kali harga sepasang sandal. Ardi membeli 2 pasang sepatu dan 3 pasang sandal dengan harga Rp420.000,00. Jika Doni membeli 3 pasang sepatu dan 2 pasang sandal, Doni harus membayar sebesar...
(A) Rp180.000,00
(B) Rp360.000,00
(C) Rp480.000,00
(D) Rp540.000,00
Jawaban:

Jadi Doni harus membayar Rp480.000,00.
- Dalam sebuah tempat parkir terdapat 90 kendaraan yang terdiri dari mobil beroda 4 dan sepeda motor beroda 2. Jika dihitung roda keseluruhan ada 248 buah. Biaya parkir sebuah mobil Rp5.000,00, sedangkan biaya parkir sebuah sepeda motor Rp2.000,00. Berapa pendapatan uang parkir dari kendaraan yang ada tersebut?
(A) Rp270.000,00
(B) Rp282.000,00
(C) Rp300.000,00
(D) Rp348.000,00
Jawaban:
Misalkan:
jumlah mobil = x
jumlah sepeda motor = y
Diketahui:
total kendaraan = 90, jadi x+y=90
jumlah roda total = 248, mobil punya 4 roda dan motor 2 roda, jadi 4x+2y=2484
Langkah penyelesaian:
1. Dari persamaan pertama kita dapat y=90−x
2. Substitusi di persamaan kedua:
4x+2(90−x)=248
4x+180−2x=248
2x=68 x=34
2x=68 x=34
3. y=90−34=56 (jumlah motor).
Biaya parkir:
mobil Rp5.000 per mobil, total Rp5.000 × 34 = Rp170.000
motor Rp2.000 per motor, total Rp2.000 × 56 = Rp112.000
Total pendapatan:
Rp170.000 + Rp112.000 = Rp282.000
Jadi, pendapatan uang parkir dari kendaraan yang ada tersebut adalah Rp282.000
- Perhatikan persamaan garis berikut
(I) 4y=16x+40
(II) 12y=24x+36
(III) 6y=24x+30
(IV) 6y=−12x+30
Pasangan garis yang sejajar adalah...
(A) (I) dan (II)
(B) (I) dan (III)
(C) (II) dan (IV)
(D) (III) dan (IV)
Jawaban:

Garis yang sejajar memiliki gradien yang sama, yaitu (I) dan (III) dengan gradien 4.
Jadi, pasangan garis yang sejajar adalah (I) dan (III).
- Bentuk sederhana dari 4x+12y−10z−8x+5y−7z adalah...
(A) −12x+12y−3z
(B) −4x+17y−17z
(C) 4x+7y−17z
(D) 12x+12y+17z
Jawaban:
Bentuk sederhana dari ekspresi 4x + 12y − 10z − 8x + 5y − 7z
dihitung dengan menjumlahkan koefisien dari variabel yang sama:
Untuk x: 4x − 8x = −4
Untuk y: 12y + 5y = 17y
Untuk z: −10z − 7z =− 17z
Jadi, bentuk sederhana dari ekspresi tersebut adalah −4x + 17y − 17z.
- Diketahui himpunan
S= {bilangan asli kurang dari 12}
A={bilangan ganjil kurang dari 11}
B={bilangan prima kurang dari 12}
Maka (A∩B)c adalah...
(A) {3,5,7}
(B) {1,2,9,11}
(C) {4,6,8,10}
(D) {1,2,4,6,8,9,10,11}
Jawaban:
Diketahui himpunan:
S = {bilangan asli kurang dari 12} = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}
A = {bilangan ganjil kurang dari 11} = {1, 3, 5, 7, 9}
B = {bilangan prima kurang dari 12} = {2, 3, 5, 7, 11}
Langkah-langkah penyelesaian:
Cari irisan A ∩ B:
A ∩ B = {3, 5, 7} (bilangan ganjil dan prima)
Lalu cari komplemen dari A ∩ B terhadap himpunan semesta S:
(A ∩ B)^c = S - (A ∩ B)
= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11} - {3, 5, 7}
= {1, 2, 4, 6, 8, 9, 10, 11}
Jadi, (A ∩ B)^c adalah himpunan {1, 2, 4, 6, 8, 9, 10, 11} sesuai himpunan komplementer terhadap S.
- Perhatikan diagram panah berikut!
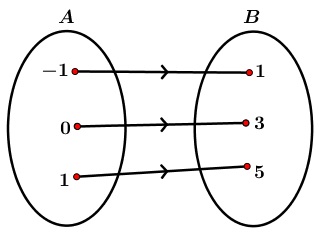
Rumus fungsi dari A ke B adalah...
(A) f(x)=−3x−2
(B) f(x)=x+2
(C) f(x)=2x+3
(D) f(x)=3x+4
Jawaban:
Pilihan yang sesuai adalah f(x)=2x+3.
- Perhatikan gambar.
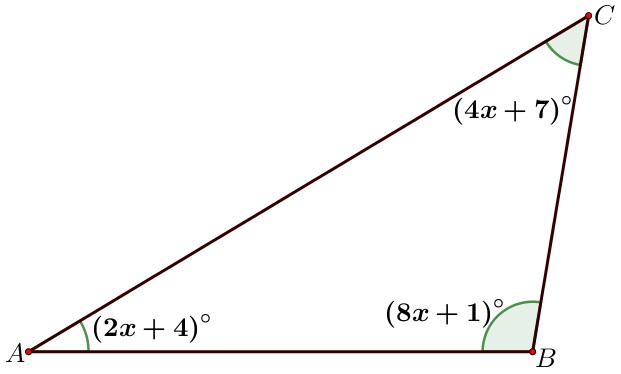
Besar sudut BAC adalah...
(A) 24∘
(B) 28∘
(C) 55∘
(D) 65∘
Jawaban:

Pilihan yang sesuai adalah
- Pada gambar berikut, segitiga PQR dan segitiga STU merupakan sua segitiga kongruen.
Besar ∠R=∠U dan ∠Q=∠S. Manakah pasangan sisi yang sama panjang?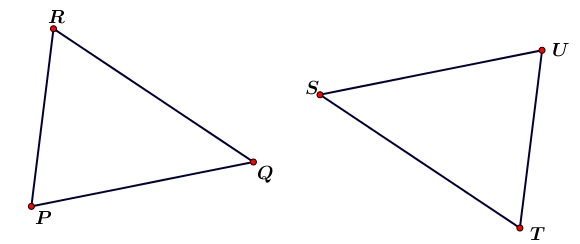
(A) PR=SU
(B) QR=TU
(C) PQ=SU
(D) PQ=ST
Jawaban:

Berdasarkan sifat segitiga kongruen, jika segitiga PQR kongruen dengan segitiga STU dengan ∠R = ∠U dan ∠Q = ∠S, maka sisi yang berhadapan dengan sudut-sudut tersebut juga sama panjang.
Sudut R berpasangan dengan sudut U, jadi sisi yang berhadapan dengan sudut R adalah PQ, dan yang berhadapan dengan sudut U adalah ST.
Sudut Q berpasangan dengan sudut S, jadi sisi yang berhadapan dengan sudut Q adalah PR, dan yang berhadapan dengan sudut S adalah TU.
Namun, dari pilihan yang ada, perbandingan sisi yang pasti sama panjang adalah sisi yang diapit oleh kedua sudut yang sama, yaitu sisi PQ dan ST.
Jadi, pasangan sisi yang sama panjang adalah PQ = ST.
- Panjang busur lingkaran dengan sudut pusat 72∘ dan panjang jari-jari 10 cm adalah...
(A) 62,80 cm
(B) 31,40 cm
(C) 12,56 cm
(D) 6,280 cm
Jawaban:

Jadi, panjang busur lingkaran adalah 12,56 cm.
- Perhatikan balok berikut!
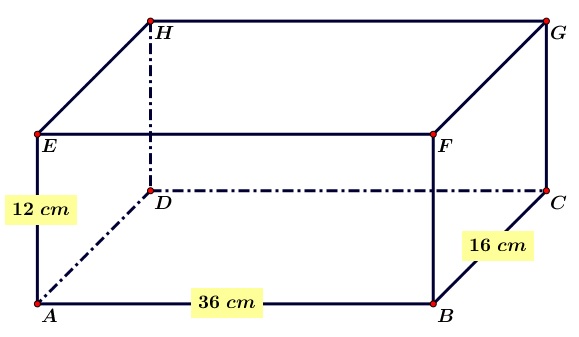
Panjang diagonal ruang DF adalah...
(A) √1696
(B) √1552
(C) √1440
(D) √400
Jawaban:

Pilihan yang sesuai adalah.