28 Soal Teori Peluang Matematika SMP dan Pembahasan

• Pada pengundian dua dadu secara bersamaan, peluang muncul mata dadu berjumlah 9 adalah...
  (A) 1/2
  (B) 1/3
  (C) 1/4
  (D) 1/9

Jawaban:

Peluang muncul mata dadu berjumlah 9 dari dua dadu dilempar sekaligus dapat dihitung dengan cara:

Jumlah ruang sampel total = 6 × 6 = 36 (karena tiap dadu memiliki 6 sisi).

Pasangan mata dadu yang jumlahnya 9 adalah:
(3, 6)
(4, 5)
(5, 4)
(6, 3)
Jumlah pasangan yang memenuhi = 4.

• Dalam suatu acara untuk memperingati Hari Kemerdekaan, ketua RT mengadakan undian berhadiah dengan hadiah utama sebuah sepeda. Jika dalam undian tersebut terdapat 300 kupon. Andi ingin mendapatkan hadiah utama dengan memiliki 15 kupon. Peluang Andi untuk mendapatkan sepeda adalah...
  (A) 1/10
  (B) 1/6
  (C) 1/20
  (D) 2/5

Jawaban:

Banyak kupon Andi untuk mendapatkan satu buah sepeda adalah 15 kupon, sehingga yang diharapak terpilih kupon diantara 15 yang dimiliki Andi, n(A)=15.

• Dalam sebuah kotak terdapat 10 bola yang diberi nomor 1 sampai 10. Diambil 3 bola satu persatu tanpa pemgembalian. Pengambilan pertama dan kedua terambil nomor ganjl. Peluang terambil bola bernomor genap pada pengambilan ketiga adalah...
  (A) 5/8
  (B) 5/10
  (C) 3/8
  (D) 3/10

Jawaban:

Diketahui dalam kotak ada 10 bola bernomor 1 sampai 10, dengan 5 bola bernomor ganjil (1, 3, 5, 7, 9) dan 5 bola bernomor genap (2, 4, 6, 8, 10).

Pengambilan dilakukan 3 kali tanpa pengembalian, dan diketahui pengambilan pertama dan kedua adalah bola nomor ganjil. Jadi, setelah dua bola ganjil terambil, tersisa:

Bola ganjil yang tersisa = 5 - 2 = 3 bola
Bola genap yang tersisa = 5 bola

Total bola tersisa = 3 + 5 = 8 bola.

• Dalam sebuah kotak terdapat 15 bola yang diberi nomor 1 sampai 15. Jika diambil 1 bola bernomor ganjil dan tidak dikembalikan, kemudian diambil lagi 1 bola bernomor genap juga tidak dikembalikan. Pengambilan ketiga diambil satu bola secara acak. Peluang terambil bola bernomor genap pada pengambilan ketiga adalah...
  (A) 7/15
  (B) 6/15
  (C) 6/13
  (D) 7/12

Jawaban:

Diketahui dalam kotak terdapat 15 bola bernomor 1 sampai 15:
Bola ganjil = 8 buah (1, 3, 5, 7, 9, 11, 13, 15)
Bola genap = 7 buah (2, 4, 6, 8, 10, 12, 14)

Pengambilan:
Bola ganjil 1 buah diambil dan tidak dikembalikan, tersisa 7 bola ganjil dan 7 bola genap.
Bola genap 1 buah diambil dan tidak dikembalikan, tersisa 7 bola ganjil dan 6 bola genap.
Pengambilan ketiga diambil satu bola secara acak dari total 13 bola tersisa.

• Roni diperbolehkan ibunya untuk mengambil satu permen dari sebuah kantong. Dia tidak dapat melihat warna permen tersebut. Banyaknya permen dengan masing-masing warna dalam kantong tersebut ditunjukkan dalam grafik berikut...
  
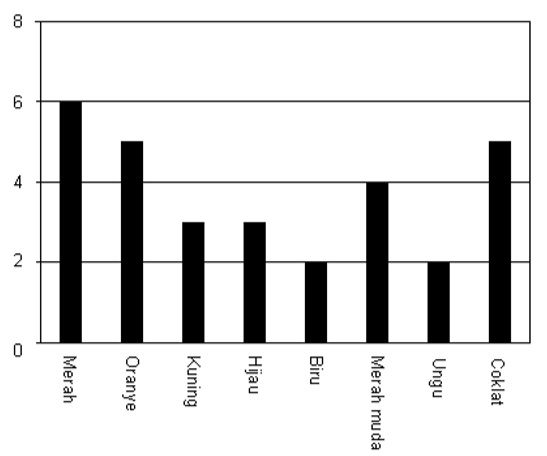
  Berapaka peluang Roni mengambil sebuah permen warna merah?
  (A) 10%
  (B) 20%
  (C) 25%
  (D) 50%

Jawaban:

Jadi, peluang Roni mengambil permen warna merah adalah 50%.

• Dalam kantong terdapat tiga bola berwarna merah diberi nomor 1−3, lima bola berwarna kuning diberi nomor 4−8 dan empat bola berwarna hijau diberi nomor 9−12. Tiga bola diambil satu persatu secara acak dari dalam kantong. Pengambilan pertama muncul bola merah bernomor genap dan tidak dikembalikan. Pengambilan kedua muncul bola hijau bernomor prima dan tidak dikembalikan. Peluang terambil bola bernomor ganjil pada pengambilan ketiga adalah...
  (A) 30%
  (B) 40%
  (C) 50%
  (D) 60%

Jawaban:

Diketahui dalam kantong terdapat bola:
    - Merah bernomor 1, 2, 3
    - Kuning bernomor 4 sampai 8
    - Hijau bernomor 9 sampai 12

Pengambilan:
   1. Pengambilan pertama muncul bola merah bernomor genap (nomor 2), bola ini tidak dikembalikan.
   2. Pengambilan kedua muncul bola hijau bernomor prima. Nomor hijau yang prima adalah 11. Bola ini juga tidak dikembalikan.
   3. Pada pengambilan ketiga, peluang terambil bola bernomor ganjil dihitung.

Sisa bola setelah dua pengambilan:
   - Bola merah tersisa: 1 dan 3 (2 bola ganjil)
   - Bola kuning: 4, 5, 6, 7, 8 (5 bola)
   - Bola hijau tersisa: 9, 10, 12 (angka 11 sudah diambil) (3 bola)
   Total bola tersisa = 2 + 5 + 3 = 10 bola.

Bola bernomor ganjil tersisa:
   - Merah ganjil = 1 dan 3 (2 bola)
   - Kuning ganjil dari 4 - 8 adalah 5 dan 7 (2 bola)
   - Hijau ganjil dari 9, 10, 12 adalah 9 saja (1 bola)
  Total bola ganjil tersisa = 2 + 2 + 1 = 5 bola ganjil.

Jadi, peluangnya adalah 50%.

• Sebuah dadu dilambungkan sekali. Peluang munculnya mata dadu genap adalah...
  (A) 1
  (B) 1/2
  (C) 1/3
  (D) 1/4

Jawaban:

Peluang munculnya mata dadu genap pada sebuah dadu yang memiliki 6 sisi (1, 2, 3, 4, 5, 6) adalah jumlah mata dadu genap dibagi total sisi dadu.

Mata dadu genap adalah 2, 4, dan 6 sebanyak 3 sisi.

• Sebuah bola diambil dari sebuah kantong yang berisi 4 bola berwarna putih, 6 bola berwarna hijau, dan 5 bola berwarna merah. Peluang terambilnya bola berwarna merah adalah...
  (A) 1/5
  (B) 4/15
  (C) 1/3
  (D) 3/5

Jawaban:

Dalam kantong terdapat total:
- 4 bola putih
- 6 bola hijau
- 5 bola merah

Total bola = 4 + 6 + 5 = 15

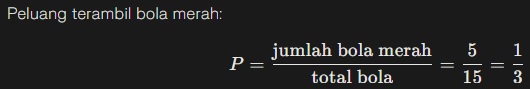
• Dua buah dadu dilambungkan bersamaan. Peluang muncul mata dadu berjumlah 4 adalah...
  (A) 1/12
  (B) 1/8
  (C) 1/6
  (D) 1/4

Jawaban:

Untuk menentukan peluang munculnya mata dadu berjumlah 4 pada pelemparan dua dadu:

Ruang sampel total dari dua dadu adalah 6×6=36

Pasangan mata dadu yang jumlahnya 4 adalah:
- (1, 3)
- (2, 2)
- (3, 1)
Jumlah pasangan yang memenuhi syarat = 3.

• Dalam kegiatan gerak jalan santai yang diikuti oleh 150 peserta, panitia menyediakan hadiah 3 buah sepeda. Peluang setiap peserta untuk mendapatkan hadiah adalah...
  (A) 0,02
  (B) 0,03
  (C) 0,20
  (D) 0,30

Jawaban:

• Dalam sebuah kantong terdapat delapan bola yang diberi nomor 1 sampai dengan 8. Akan diambil sebuah bola secara acak. Peluang terambilnya bola bernomor lebih dari 6 adalah...
  (A) 2/8
  (B) 3/8
  (C) 4/8
  (D) 5/8

Jawaban:

Peluang terambilnya bola bernomor lebih dari 6 dari sebuah kantong yang berisi bola bernomor 1 sampai 8 adalah:

• Bola bernomor lebih dari 6 adalah bola nomor 7 dan 8, itu berarti ada 2 bola.

• Total bola dalam kantong adalah 8.

Maka, peluangnya dihitung dengan membagi jumlah bola bernomor lebih dari 6 dengan total bola, yaitu:

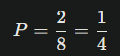
Namun, pilihan jawaban yang tersedia adalah:
(A) 2/8
(B) 3/8
(C) 4/8
(D) 5/8

Karena 2/8 sama dengan pilihan (A), jawaban yang benar adalah: (A) 2/8

• Tiga keping uang logam dilempar bersama-sama. Peluang muncul ketiganya gambar adalah...
  (A) 1/8
  (B) 1/3
  (C) 3/8
  (D) 2/3

Jawaban:

Peluang muncul ketiganya gambar pada pelemparan tiga keping uang logam adalah perbandingan jumlah kejadian muncul tiga gambar dengan total kemungkinan hasil.

• Total kemungkinan hasil pelemparan tiga keping uang logam adalah 2³=8 (karena tiap keping punya dua sisi: gambar dan angka).

• Hanya ada satu kejadian muncul ketiganya gambar, yaitu {GGG}.

Sehingga peluang muncul ketiganya gambar adalah 1/8.

• Sebuah dadu dilambungkan satu kali. Peluang munculnya mata dadu kurang dari 4 adalah...
  (A) 1/6
  (B) 1/3
  (C) 1/2
  (D) 2/3

Jawaban:

Peluang munculnya mata dadu kurang dari 4 pada pelemparan satu kali adalah peluang muncul angka 1, 2, atau 3.
- Ada 3 angka yang kurang dari 4 (yaitu 1, 2, 3).
- Total kemungkinan angka pada dadu adalah 6 (angka 1 sampai 6).
Jadi, peluangnya adalah:

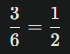
Jawaban yang benar adalah 1/2.

• Dalam satu kelas dilakukan pendataan peserta ekstrakurikuler. Didapat hasil sebagai berikut:
  9 siswa memilih pramuka
  12 siswa memilih volly
  7 siswa memilih PMR
  8 siswa memilih KIR
  Dipilih seorang siswa secara acak untuk dijadikan koordinator ekstrakurikuler, kemungkinan yang terpilih siswa dari cabang volly adalah...
  (A) 1/12
  (B) 1/6
  (C) 1/3
  (D) 2/2

Jawaban:

Total siswa yang mengikuti ekstrakurikuler adalah:

- Pramuka: 9 siswa
- Volly: 12 siswa
- PMR: 7 siswa
- KIR: 8 siswa

Jumlah total siswa = 9 + 12 + 7 + 8 = 36 siswa.

Peluang terpilihnya siswa dari cabang volly adalah jumlah siswa volly dibagi total siswa, yaitu:

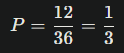
Jadi, kemungkinan terpilihnya siswa dari cabang volly adalah 1/3.

• Seorang ibu dan anaknya bermain tebak warna dengan cara mengambil bola dari sebuah kotak A dan memasukkannya kembali ke kotak B. Kotak A beirisi 5 bola merah, 7 bola kuning dan 3 bola biru, sedangkan kotak B berisi 3 bola merah, 5 bola kuning dan 3 bola biru. Aturan permainannya adalah pada pengambilan pertama ibu akan mengambil bola dari kotak a dan memasukkanya ke kotak B, dilanjutkan dengan pada pengambilan kedua si anak akan mengambil satu bola dari kotak B dan memasukkanya ke kotak A. Peluang kejadian terambilnya bola warnanya sama pada setiap pengambilan bola adalah...
  (A) 37/90
  (B) 38/90
  (C) 39/90
  (D) 37/90

Jawaban:

Peluang kejadian terambilnya bola dengan warna yang sama pada setiap pengambilan bola bisa dihitung dengan menjumlahkan peluang terambilnya bola merah, bola kuning, dan bola biru pada dua pengambilan berurutan.

Diketahui:
Kotak A: 5 merah, 7 kuning, 3 biru (total 15)
Kotak B: 3 merah, 5 kuning, 3 biru (total 11)

Langkahnya:

1. Peluang memilih bola merah di A dan memindahkan ke B, lalu mengambil bola merah dari B:

 

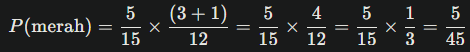
2. Peluang memilih bola kuning di A dan memindahkan ke B, lalu mengambil bola kuning dari B:

 

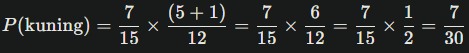
3. Peluang memilih bola biru di A dan memindahkan ke B, lalu mengambil bola biru dari B:

 

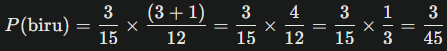
Total peluang kejadian warna sama adalah:

 

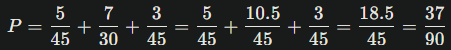
Jadi, peluang kejadian terambilnya bola dengan warna yang sama pada setiap pengambilan adalah 37/90.

• Sebuah keluarga ingin mempunyai 4 orang anak. Peluang bahwa keluarga tersebut memiliki paling banyak 2 orang anak laki-laki adalah...
  (A) 5/16
  (B) 11/16
  (C) 14/16
  (D) 15/16

Jawaban:

Untuk menjawab peluang bahwa sebuah keluarga yang memiliki 4 orang anak memiliki paling banyak 2 anak laki-laki, diperlukan menggunakan distribusi binomial.

Distribusi binomial:

Dimana:

• $n=4$ (jumlah anak)

• $p=\genfrac{}{}{0ex}{}{1}{2}$ (asumsi peluang anak laki-laki atau perempuan sama)

• $x$ = jumlah anak laki-laki

Peluang "paling banyak 2 anak laki-laki" berarti x=0,1,2:

$P(X\le 2)=P(X=0)+P(X=1)+P(X=2)$

Hitung satu persatu:

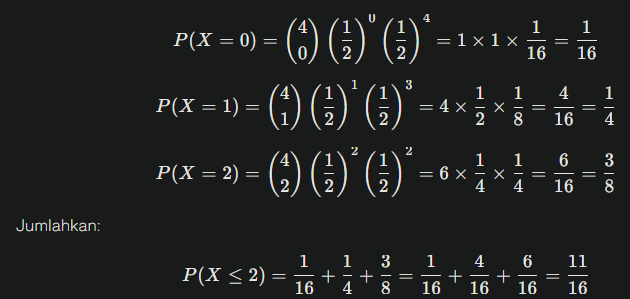
Jadi, peluang bahwa keluarga tersebut memiliki paling banyak 2 anak laki-laki adalah 11/16.

• Diberikan gambar berikut (lingkaran di dalam lingkaran).

Jika diambil sebuah titik secara acak, peluang terambilnya titik dari daerah yang tidak diarsir adalah...
(A) 0,12
(B) 0,36
(C) 0,42
(D) 0,64

Jawaban:

Untuk menghitung peluang terambilnya titik dari daerah yang tidak diarsir pada gambar lingkaran dalam lingkaran, kita perlu mengetahui luas daerah yang tidak diarsir dibandingkan dengan luas total lingkaran luar.

Namun ini tidak ada di pilihan.

Jika misal jari-jari dalam adalah sekitar 0,8 dari jari-jari luar:

Maka jawaban yang paling sesuai adalah 0,36.

• Dua buah dadu dilempar bersamaan. Peluang munculnya dua mata dadu berbeda adalah...
  (A) 1/6
  (B) 1/2
  (C) 3/4
  (D) 5/6

Jawaban:

Peluang munculnya dua mata dadu berbeda saat dua buah dadu dilempar bersamaan adalah:

• Total kemungkinan hasil dari pelemparan dua dadu adalah 6×6=36.

• Kemungkinan munculnya dua mata dadu yang sama ada 6 (yaitu (1,1), (2,2), ..., (6,6)).

• Jadi, kemungkinan muncul dua mata dadu yang berbeda adalah 36−6=30.

Peluangnya adalah:

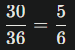
Jadi, jawaban yang benar adalah 5/6.

• Babak perempat final Liga Champion 2021 diikuti oleh 8 tim A,B,C,D,E,F,G, dan H yang berlaga dan ditentukan dengan hasil undian sebagai berikut.

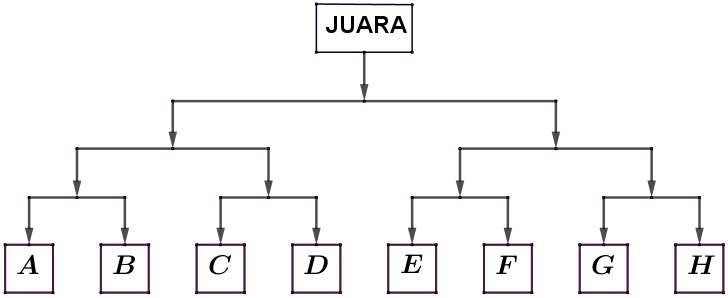
Setiap tim memiliki peluang 12 untuk melaju ke babak selanjutnya. Peluang B bertemu F di babak final dan F menjadi juara adalah...
(A) 1/2
(B) 1/4
(C) 1/16
(D) 1/32

Jawaban:

Peluang B bertemu F di babak final dan F menjadi juara dapat dihitung dengan langkah berikut:

1. Peluang lolos dari babak perempat final untuk setiap tim adalah 1/2.

2. Agar B dan F bertemu di babak final, keduanya harus lolos dari perempat final dan semifinal.

3. Peluang B lolos dari perempat final dan semifinal adalah (1/2) × (1/2) = 1/4.

4. Peluang F melakukan hal yang sama juga 1/4.

5. Peluang keduanya bertemu di final adalah 1/4 × 1/4 = 1/16.

6. Kemudian peluang F menjadi juara adalah 1/2 (karena peluang menang di final 50%).

Jadi, peluang B bertemu F di final dan F menjadi juara adalah:

 

Jawabannya adalah 1/32.

• Seorang siswa mempunyai tiga buah celana berwarna biru, hitam dan abu-abu, tiga buah kemeja berwarna putih, hijau dan kuning serta dua pasang sepatu berwarna hitam dan coklat. Banyak kombinasi pakain dan sepatu yang bisa digunakan siswa tersebut adalah .. kombinasi.
  (A) 12
  (B) 15
  (C) 18
  (D) 24

Jawaban:

• Dua dadu bermata 6 dilempar sekali secara secara bersamaan, peluang muncul mata dadu berjumlah 7 adalah...
  (A) 1/6
  (B) 1/3
  (C) 1/2
  (D) 2/3

Jawaban:

Peluang munculnya jumlah mata dadu 7 saat dua dadu bermata 6 dilempar sekaligus adalah 1/6.

• Dalam sebuah peti terdapat 7 bola kuning bernomor 1−7, dan 5 bola merah bernomor a−e. Jika seseorang mengambil sebuah bola dari dalam peti secara acak, peluang terambilnya bola kuning bernomor ganjil atau bola merah dengan huruf vokal adalah...
  (A) 1/2
  (B) 1/3
  (C) 1/6
  (D) 1/12

Jawaban:

Untuk menentukan peluang terambilnya bola kuning bernomor ganjil atau bola merah dengan huruf vokal dari peti:

• Jumlah bola kuning: 7 (nomor 1-7)

• Bola kuning bernomor ganjil: nomor 1, 3, 5, 7 → 4 bola

• Bola merah: 5 bola bernomor a-e

• Huruf vokal dari a-e adalah a dan e → 2 bola merah

Total bola dalam peti: 7 + 5 = 12
Jumlah bola yang diinginkan: 4 (kuning ganjil) + 2 (merah vokal) = 6 bola

Peluangnya adalah

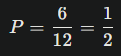
Jadi, jawabannya adalah 1/2.

•  Sebuah dadu dilempar sebanyak 120 kali. Frekuensi harapan munculnya mata dadu bilangan prima adalah...
  (A) 60 kali
  (B) 40 kali
  (C) 30 kali
  (D) 20 kali

Jawaban:

Frekuensi harapan munculnya mata dadu bilangan prima saat sebuah dadu dilempar sebanyak 120 kali dapat dihitung sebagai berikut:

• Bilangan prima pada dadu adalah 2, 3, dan 5, jadi ada 3 bilangan prima dari 6 kemungkinan hasil.

• Peluang muncul bilangan prima adalah 3/6 = 1/2.

• Frekuensi harapan = peluang × banyak percobaan = 1/2 × 120 = 60 kali.

Jadi, frekuensi harapan munculnya mata dadu bilangan prima adalah 60 kalii.

• Suatu koin dilempar sebanyak 100 kali. Jika kemunculan mata koin angka sebanyak 40 kali, peluang empirik kemunculan mata koin angka adalah...
  (A) 40/60
  (B) 60/40
  (C) 2/5
  (D) 1/2

Jawaban:

Jadi, peluang empirik kemunculan mata koin angka adalah 2/5.

• Sebuah kantong berisi 5 kelereng merah, 6 kelereng kuning, dan 9 kelereng hijau. Sebuah kelereng diambil dari kantong tersebut. Peluang terambil kelereng kuning adalah...
  (A) 6/9
  (B) 6/10
  (C) 6/5
  (D) 3/10

Jawaban:

Jadi, jawabannya adalah 3/10.

• Berikut ini terdapat $11$ koin yang bertuliskan bilangan-bilangan.

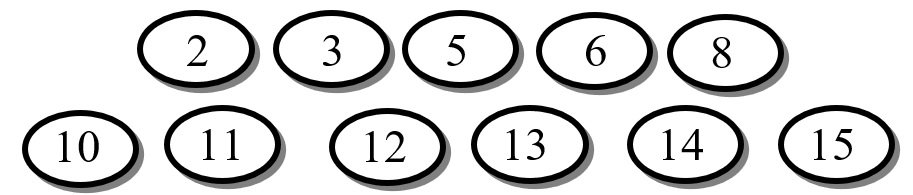
Dedi mengambil suatu koin tanpa melihat. Peluang Dedi mendapatkan koin yang bertuliskan bilangan kelipatan 2 adalah...
(A) 1/11
(B) 2/11
(C) 5/11
(D) 6/11

Jawaban:

Banyak koin ada $11$ koin sehingga $n\left(S\right)=11$.

Kejadian $\left(E\right)$ yang diharapkan adalah terambil koin kelipatan $2$ yaitu $2,6,8,10,12,14$ maka $n\left(E\right)=6$.

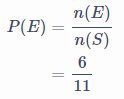
Pilihan yang sesuai adalah$\frac{\mathrm{6/}}{11}$.

• Dalam rangka memperingati Hari Kemerdekaan RI yang ke-80, sekolah mengadakan undian doorprize bagi seluruh murid. Panitia menyiapkan sebuah kotak berisi kartu yang diberi nomor $1$ sampai dengan $30$.
  Aturan pengambilan udian: "setiap peserta hanya boleh mengambil satu kartu, dan yang mendapatkan kartu bernomor kelipatan $3$ atau bilangan prima" akan mendapat hadiah doorprize.

Berapakah peluang seorang murid akan mendapatkan doorprize?
(A) 10/30
(B) 19/30
(C) 20/30
(D) 21/30

Jawaban:

Dari informasi pada soal, kotak berisi kartu yang diberi nomor $1$ sampai dengan $30$ sehingga pada teori peluang ini kita sebut dengan hasil yang mungkin, anggotanya adalah $n\left(S\right)=30$.

Yang mendapatkan hadiah kartu bernomor kelipatan $3$, $E:\{3,6,9,12,15,18,21,24,27,30\}ataubilanganprima$E:\{2,5,7,11,13,17,19,23,29\}, ini kita sebut yang diharapkan terjadi, sehingga $n\left(E\right)=10+9=19$.

• Sebuah survei mengambil secara acak 60 murid sebagai sampelnya. Pertayaan yang diberikan adalah "apakah mereka membawa bekal ke sekolah?". Hasilnya, 36 siswa menjawab "Ya" sedang lainnya "Tidak". Jika survei dilakukan lagi pada 50 murid lainnya dan diperkirakan hasil survey sama proporsinya dengan survey sebelumnya, frekuensi relatif murid yang membawa bekal dari seluruh siswa yang disurvei adalah....
  (A) 0,59
  (B) 0,60
  (C) 0,61
  (D) 0,62

Jawaban:

 

Frekuensi relatif adalah perbandingan jumlah kejadian dengan total data yang ada. Dalam survei pertama, dari 60 murid, 36 membawa bekal, sehingga proporsi membawa bekal adalah 36/60 = 0,6.

Jika survei dilakukan ulang pada 50 murid dengan proporsi yang sama, maka jumlah murid yang membawa bekal adalah 0,6 × 50 = 30.

Total murid yang disurvei seluruhnya = 60 + 50 = 110
Jumlah total murid yang membawa bekal = 36 + 30 = 66

Frekuensi relatif murid yang membawa bekal dari seluruh siswa survei adalah:

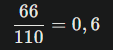
Jadi, frekuensi relatifnya adalah 0,60, sehingga jawabannya adalah (B) 0,60.