15 Contoh Soal TKA Matematika SMP dan Penjelasan Materinya

• Umur ayah 3 kali umur anaknya. Lima tahun yang akan datang, jumlah umur mereka adalah 70 tahun. Manakah model matematika yang tepat untuk situasi ini, jika umur ayah = A dan umur anak = B?
  A = 3B
  B. (A + 5) + (B + 5) = 70
  C. A + B + 10 = 70
  D. Umur anak sekarang adalah 15 tahun

Jawaban:

Model matematika yang tepat untuk situasi ini dengan umur ayah = A dan umur anak = B adalah:

    - Umur ayah adalah 3 kali umur anak, sehingga:

      A=3B

    - Lima tahun yang akan datang, jumlah umur mereka adalah 70 tahun, sehingga:

      (A+5)+(B+5)=70

Persamaan ini dapat disederhanakan menjadi:

    A+B+10=70

Jadi, model matematikanya adalah:

   A=3B

   A+B+10=70

• Hasil dari -5 + 8 × 2 adalah...
  A. 6
  B. 11
  C. -6
  D. -13

Jawaban:

Hasil dari -5 + 8 × 2 dihitung dengan aturan urutan operasi (PEMDAS), di mana perkalian dilakukan sebelum penjumlahan.

Langkahnya:

    Hitung 8 × 2 = 16

    Kemudian -5 + 16 = 11

Jadi, hasilnya adalah 11.

• Diketahui 2a = 3 dan 3b = 4, maka nilai dari a × b adalah...
  A. 1
  B. 2
  C. 3
  D. 4

Jawaban:

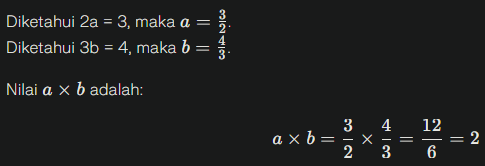
Jadi, nilai $a\times b$ adalah 2.

• Sebuah akuarium berbentuk balok memiliki ukuran panjang 50 cm, lebar 30 cm, dan tinggi 40 cm. Berapa volume air yang dibutuhkan untuk mengisinya penuh?
  A. 6.000 cm³
  B. 12.000 cm³
  C. 60.000 cm³
  D. 120.000 cm³

Jawaban:

Volume balok dihitung dengan rumus:
V = p × l × t

di mana pp adalah panjang, ll adalah lebar, dan tt adalah tinggi balok.
Diketahui panjang = 50 cm, lebar = 30 cm, dan tinggi = 40 cm, maka:
V = 50 × 30 × 4 0= 60.000cm³

Jadi, volume air yang dibutuhkan untuk mengisi akuarium tersebut penuh adalah 60.000 cm³.

• Bentuk paling sederhana dari 18/24 adalah...
  A. 3/4
  B. 6/8
  C. 2/3
  D. 4/5

Jawaban:

Bentuk paling sederhana dari pecahan 18/24 diperoleh dengan mencari faktor persekutuan terbesar (FPB) dari 18 dan 24.

Faktor dari 18: 1, 2, 3, 6, 9, 18
Faktor dari 24: 1, 2, 3, 4, 6, 8, 12, 24
FPB dari 18 dan 24 adalah 6.

Kemudian, bagi pembilang dan penyebut dengan FPB:

Jadi, bentuk paling sederhana dari 18/24 adalah 3/4.

• Harga setengah kilogram cabai rawit adalah Rp35.000. Jika Ibu membeli 2¼ kilogram, maka total harganya adalah...
  A. Rp175.000
  B. Rp157.500
  C. Rp140.000
  D. Rp87.500

Jawaban:

Harga setengah kilogram cabai rawit adalah Rp35.000, jadi harga per kilogram adalah:
      Harga per kg = 2 × 35.000 = Rp70.000

Ibu membeli 2¼ kilogram, yang sama dengan 2.25 kg.

Total harga yang harus dibayar adalah:
      70.000 × 2.25 = Rp157.500

Jadi, total harga yang harus dibayar adalah Rp157.500

• Misalkan a dan b memenuhi sistem persamaan berikut:
  2x + ay = 4
  bx - 2y = -1
  Jika (x, y) = (5, 2), tentukan pernyataan yang benar!
  A. a merupakan bilangan prima
  B. b merupakan bilangan ganjil
  C. 10a + b = 31

Jawaban:

• Diketahui pita merah sepanjang 12 m, pita hijau 8 m, dan pita kuning 7,5 m. Pita kuning dipotong menjadi 20 bagian, pita hijau 25 bagian, dan pita merah 50 bagian. Manakah pernyataan yang benar?
  A. Potongan pita kuning lebih panjang daripada pita merah
  B. Potongan pita merah lebih panjang daripada pita hijau
  C. Potongan pita hijau lebih pendek daripada pita kuning
  D. Potongan pita hijau sama panjang dengan pita kuning

Jawaban:

• Toko Mbahe Murah memberi diskon 10% untuk 1 baju, dan 15% untuk 2 baju sejenis. Harga baju A Rp250.000 dan baju B Rp125.000.
  A. Pinto membeli 1 baju A, bayar Rp225.000
  B. Santi membeli 2 baju B, bayar Rp212.500
  C. Dewanti membeli 1 baju A dan 1 baju B, bayar Rp327.500

Jawaban:

Mari hitung harga yang harus dibayar untuk setiap pernyataan:

Pinto membeli 1 baju A seharga Rp250.000 dengan diskon 10%.
Diskon = 10% × 250.000 = 25.000
Harga bayar = 250.000 - 25.000 = Rp225.000
Jadi pernyataan A benar.

Santi membeli 2 baju B masing-masing seharga Rp125.000 dengan diskon 15%.
Total harga awal = 2 × 125.000 = 250.000
Diskon = 15% × 250.000 = 37.500
Harga bayar = 250.000 - 37.500 = Rp212.500
Jadi pernyataan B benar.

Dewanti membeli 1 baju A dan 1 baju B, masing-masing dengan diskon 10% karena satuan.
Harga baju A setelah diskon = 250.000 - 10% × 250.000 = 225.000
Harga baju B setelah diskon = 125.000 - 10% × 125.000 = 112.500
Total bayar = 225.000 + 112.500 = 337.500
Jadi pernyataan C salah (bukan Rp327.500).

Kesimpulan: Pernyataan yang benar adalah A dan B.

• Jika titik A(3, -5) ditranslasikan oleh T(2, 7), maka koordinat bayangan titik A adalah...
  A. A'(5, 2)
  B. Absis bayangan 5
  C. Ordinat bayangan 2
  D. Berada di kuadran IV

Jawaban:

Jadi, jawaban yang benar adalah: A. A'(5, 2).

• 25 persen dari 80 adalah...
  A. 10
  B. 20
  C. 25
  D. 15

Jawaban:

25 persen dari 80 dihitung dengan rumus:

Jadi, 25 persen dari 80 adalah 20.

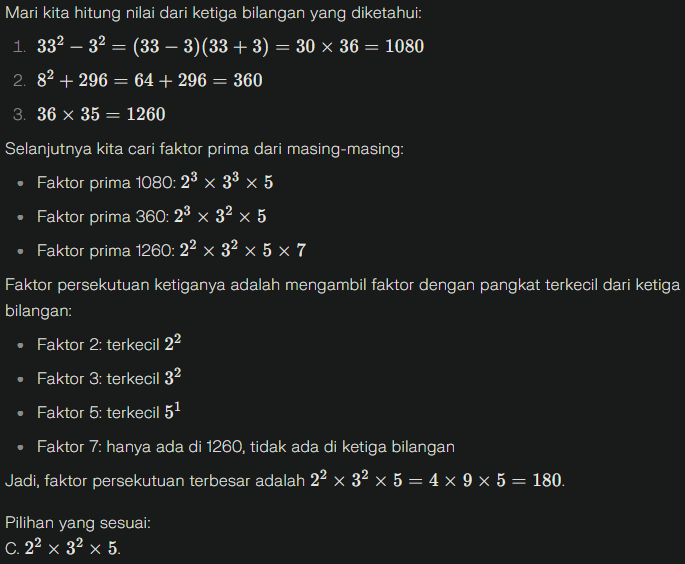
• Diketahui 33² − 3², 8² + 296, dan 36 × 35. Bilangan apa saja yang merupakan faktor persekutuan ketiga bilangan tersebut?
  A. 2³ × 3³ × 7
  B. 2² × 3² × 7
  C. 2² × 3² × 5
  D. 2 × 3² × 5

Jawaban:

• Rata-rata berat telur kecil 45 g, sedang 55 g, besar 65 g. Dalam satu kemasan berisi 1 telur besar, 5 telur sedang, dan 2 telur kecil. Dua telur tambahan apa yang harus dipilih agar rata-rata tetap 55 g?
  A. 2 telur sedang
  B. 2 telur besar
  C. 1 telur besar dan 1 telur kecil
  D. 1 telur besar dan 1 telur sedang

Jawaban:

Diketahui:
Rata-rata berat telur kecil = 45 g
Rata-rata berat telur sedang = 55 g
Rata-rata berat telur besar = 65 g

Dalam satu kemasan ada:
1 telur besar
5 telur sedang
2 telur kecil

Hitung total berat dalam satu kemasan awal:
1 × 65 + 5 × 55 + 2 × 45 = 65 + 275 + 90 = 430gram

Jumlah telur awal:
1+5+2=8 butir

Rata-rata berat awal:

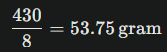
Dua telur tambahan yang dipilih harus membuat rata-rata menjadi 55 g, dengan jumlah telur menjadi 10.

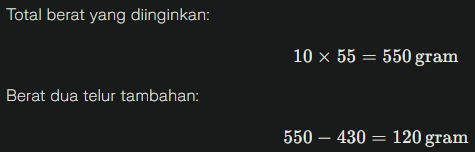
Pilih dua telur yang total beratnya 120 gram dari pilihan:

2 telur sedang: 2 × 55 = 110
2 telur besar: 2 × 65 = 130
1 telur besar + 1 telur kecil: 65 + 45 = 110
1 telur besar + 1 telur sedang: 65 + 55 = 120

Jadi, pilihan yang benar adalah:
D. 1 telur besar dan 1 telur sedang

• Bu Dhias memiliki 2½ kg tepung protein tinggi dan 1¾ kg protein sedang. Setelah menambah 2,5 kg dan 1,25 kg lagi, total adonan jadi 6,2 kg. Berapa sisa tepungnya?
  A. 1⅕ kg
  B. 1⅖ kg
  C. 1¾ kg
  D. 1⅘ kg

Jawaban:

• Penyelesaian dari sistem persamaan berikut adalah...
  x – 2y = 10
  3x + 2y = -2
  A. x = 2, y = -4
  B. x = -2, y = 4
  C. x = 4, y = -3
  D. x = -4, y = 2

Jawaban:

Langkah penyelesaian menggunakan metode eliminasi:

Jadi, penyelesaiannya adalah $x=2$, $y=-4$, yang sesuai dengan pilihan A.